Никакое словесное объяснение никогда не заменит созерцания…
Антуан де Сент-Экзюпери.

 

           Мир физики многогранен, но начинается он с механики…а точнее даже с кинематики. Человечество сначала жило без наук, в том числе и без физики. Но…Физика напоминала о себе на каждом шагу…Надо доставить груз, а как это сделать проще? И изобретается колесо…Сначала человек изучал само явление движения, т.е. как добраться из пункта А в пункт В, и, желательно, побыстрее…

 

 

 

«Механика — это не детство физики, это душа физики».  Столетов.

 

Основные понятия механики.

 

 

        Любое физическое явление или процесс в окружающем нас материальном мире представляет собой закономерный ряд изменений, происходящих во времени и пространстве. Механическое движение, то есть изменение положения данного тела (или его частей) относительно других тел, – это простейший вид физического процесса.

             Механическое движение тел изучается в разделе физики, который называется механикой.

Её основная задача — определить положение тела  в любой момент времени.

               Механика — одна из древних наук.  Определенные сведения в этой отрасли были известны еще в глубокой древности. (Аристотель (IV в. до н. э.), Архимед (IIIв. до н.э.)).  Однако количественное изучение механики началось только в  в XVIIв, когда Г. Галилей  (1954-1962)  открыл кинетический закон сложения скоростей и установил законы свободного падения тел.  Спустя несколько десятилетий после этого  И. Ньютон (1643-1727) сформулировал основные законы динамики.  

                В механике Ньютона движение тел рассматривается при скоростях намного меньших, скорости света в  пустоте.  Эту механику называют классической или ньютоновской механикой, в отличии от релятивистской механики, созданной в начале XX века, главным образом благодаря работам А. Эйнштейна ( 1879-1956).  В релятивистской механике движение тел рассматривается при скоростях близких к скорости света.  Классическая механика Ньютона является предельным случаем релятивистской механики при v

 

           Каждое тело в любой момент времени занимает определенное положение в пространстве относительно других тел. Если с течением времени положение тела не изменяется, то говорят, что тело находится в покое.        

        Если же с течением времени положение тела изменяется, то это значит, что тело совершает механическое движение.

           Механическим движением тела называется изменение его положения в пространстве относительно других тел с происходящее с течением времени.

 

      *  При решении различных научных и практических задач, связанных с механическим движением тел,  нужно уметь описывать это движение, т.е. определять траекторию, скорость, пройденный путь, положение тела и некоторые другие характеристики движения для любого момента времени. *

          Изучить движение тела — значит узнать, как изменяется его положение с течением времени. Если это известно, то можно вычислить положение тела в любой момент времени.

        В этом и состоит основная задача механики — определять положение тела в любой момент времени.

           Так, астрономы, пользуясь законами механики, могут вычислять положения небесных тел друг относительно друга и с большой точностью предсказывать такие небесные явления, как затмения Солнца или Луны.

       Тела могут совершать разнообразные механические движения: двигаться по разным траекториям, быстрее или медленнее и т. д. Чтобы решить основную задачу механики, нужно кратко и точно указать, как движется тело, как изменяется его положение с течением времени. Другими словами, надо найти математическое описание движения, установить связь между величинами, характеризующими движение.

          Эти величины и связи между ними мы рассмотрим в первом разделе механики, называемом кинематикой. 

 

          §1. Поступательное движение тел. Материальная точка.

         Чтобы изучать движение тела, т.е. изменение положения тела в пространстве, нужно прежде всего уметь определять это положение.

Но здесь возникает затруднение…

         Каждое тело имеет определённые размеры, и, следовательно, различные токи тела находятся в разных местах пространства. Как же определить положение тела?  Всех его точек?

     Но оказывается, во многих случаях нет необходимости указывать положение каждой точки движущегося тела.

    Этого не нужно делать, когда все точки движутся одинаково.

     Зачем, например, описывать движение каждой точки санок, которые мальчик тянет в гору, если эти движения ничем не различаются между собой.  Одинаково движутся все точки чемодана, который мы поднимаем с пола  (рис.1), кабины аттракциона «колесо обозрения» в парке, ступеньки эскалатора в метрополитене, и т.д.

          При таком движении, любая прямая, мысленно проведенная в теле, остается параллельной сама себе.  Можно так сказать:  тело движется поступательно, если оно одновременно не вращается и не вращается и даже не поворачивается.        

          Движение тела, при котором все его точки движутся одинаково, называется поступательным.

        Не нужно описывать движение каждой точки и тогда, если размеры тела малы, по сравнению с расстоянием, которое оно  проходит.  Например, океанский лайнер мал по сравнению с протяженностью его рейса, поэтому, при описании его движения в океане, корабль можно считать точкой.

           Так поступают и  астрономы при описании движения небесных тел.  Планеты, звезды, солнце, конечно, не малые тела.  Но радиус Земли, например, примерно в 24000 раз меньше, чем расстояние от Земли до Солнца.    Поэтому Землю можно считать точкой, движущейся вокруг другой точки – центра Солнца.

           В дальнейшем, говоря о движении тела,  мы, в действительности  будем иметь в виду движение какой-то одной его  точки.  Но не надо забывать при этом, что материальная точка отличается от тела только тем, что она не имеет размеров.

       Тело, размерами которого можно  в данных условиях движения можно пренебречь, называют материальной точкой.

 

---

к

            Указать положение материальной точки в реальном   физическом пространстве можно лишь относительно положения других тел. 

 

           Тело отсчёта — произвольно выбранное тело, относительно которого определяется положение движущейся материальной точки (или тела).

 

Траектория.  Очень  важным понятием при описании движения тела является траектория — последовательность точек (линия), в которых находилось тело в процессе своего движения.

———————-к

2. Основные понятия кинематики.

                  

          Итак:  Кинематикой называют раздел механики, в котором движение тел рассматривается без выяснения причин, его вызывающих. Механическим движением тела называют изменение его положения в пространстве относительно других тел с течением времени.   

         Кинематика — это раздел механики, изучающий способы описания движений и связь между величинами, характеризующими эти движения.

Описать движение тела, — это  значит определение его положения  в пространстве в любой момент времени.

       Механическое движение относительно.   Движение одного и того же тела относительно разных тел оказывается различным.  Для описания движения тела нужно указать, по отношению  к какому телу  рассматривается движение.   Это тело называют телом отсчета.

          Чтобы определить, как тело движется с течением времени нужен момент отсчета, т.е. часы.

 

         Система координат, связанная с телом отсчета, и часы для отсчета времени  образуют систему отсчета, позволяющую определять положение движущегося тела в любой момент времени.  

 

(или так:

 

            Для определения  положения движущегося тела в любой момент времени, вида движения, скорости тела и некоторых других характеристик движения необходимы  тело отсчета, связанная с ним система координат (или одна координатная ось, если тело движется вдоль прямой) и прибор для измерения времени.

---

          Система координат, тело отсчета, с которым она связана и прибор для измерения времени образуют систему отсчета,  относительно которой рассматривается движение тела.

---

)

 

 

Пример:

Зависимость траектории от тела отсчёта:

   В Международной системе единиц (СИ) за единицу длины принят метр, а за единицу времени – секунда. 

          Всякое тело имеет определенные размеры. Различные части тела находятся в разных местах пространства. Однако, во многих задачах механики нет необходимости указывать положения отдельных частей тела. Если размеры тела малы по сравнению с расстояниями до других тел, то данное тело можно считать материальной точкой, т.е. точкой, обладающей массой этого тела.

 Так можно поступать, например, при изучении движения планет вокруг Солнца.  

          Для материальной точки можно однозначно определить координату, скорость и другие физические величины, т.к. она не имеет размеров и не может вращаться вокруг собственной оси.              Материальных точек нет в природе. Материальная точка — это понятие, использование которого упрощает решение многих задач и при этом позволяет получить достаточно точные результаты.

 

Тело можно считать материальной точкой в тех случаях, когда его размерами (а значит, и формой, и вращением) можно пренебречь, поскольку они несущественны в условиях решаемой задачи.

 

Если все части тела движутся одинаково, то такое движение называется поступательным. Поступательно движется, например, автомобиль на прямолинейном участке пути.При поступательном движении тела его также можно рассматривать как материальную точку.   

 

---

Материальная точка — это понятие, вводимое в механике для обозначения тела,  которое рассматривается как точка, имеющая массу.

---

---

          Тело, размерами которого в данных условиях можно пренебречь, называется материальной точкой.    

—————————————————————————————————————————————————————————

Понятие материальной точки играет важную роль в механике. Перемещаясь с течением времени из одной точки в другую, тело (материальная точка) описывает некоторую линию, которую называют   траекторией движения тела. 

            Перемещением тела     называют направленный отрезок прямой, соединяющий начальное положение тела с его последующим положением. Перемещение есть векторная величина.

Пройденный путь l равен длине дуги траектории, пройденной телом за некоторое время t. Путь – скалярная величина.

         В случае достаточно малого промежутка времени Δt пройденный телом путь Δl почти совпадает с модулем вектора перемещения . При движении тела по криволинейной траектории модуль вектора перемещения всегда меньше пройденного пути (рис. 2).

 

 

 

 

 

 

 

 

 

Рисунок 2.

Пройденный путь     и вектор перемещения    при криволинейном движении  тела. а и b  начальная и конечная точки пути.

 

 

Рис. 3. Аналогично, криволинейное движение из точки М1 в т. М2.

 

          Перемещением тела  называют направленный отрезок прямой, соединяющий начальное положение тела с его последующим положением. Перемещение есть векторная величина.

       Пройденный путь Ι равен длине дуги траектории, пройденной телом за некоторое время t. Путь – скалярная величина.

 

Переходя к кинематике удобно представить разные виды движений в виде такой схемы:

 

         Наша задача при рассмотрении движения тела — научиться рассчитывать положение тела в любой момент относительно тела отсчета.

 

        § 2.          Рассмотрим разные виды движений согласно приведенной схеме, но раньше поговорим о координатах.

ПОЛОЖЕНИЕ ТЕЛА В ПРОСТРАНСТВЕ.  КООРДИНАТЫ.  СИСТЕМЫ КООРДИНАТ.

              Существуют несколько способов описания, или, что одно и то же, задания, движения точки.  Рассмотрим два из них. которые наиболее часто встречаются.

КООРДИНАТНЫЙ СПОСОБ.

 

Будем задавать положение точки с помощью координат, как на рисунке.  Если точка (тело) движется, то её координаты изменяются с течением времени. Так как координаты точки зависят от времени, то можно сказать, что они являются функциями времени.  Математически это принято записывать в виде:

               Уравнения называются кинематическими  уравнениями движения точки, записанными в координатной форме.   Если они известны, то для каждого момента времени мы можем рассчитать

координаты точки, а следовательно, её положение относительно выбранного тела отсчета.

           Вид уравнений для каждого конкретного  движения будет вполне определенный.

           Линия, по которой движется точка в пространстве, называется траекторией.

           В зависимости от формы траектории, все движения точки делятся на прямолинейные и криволинейные.  Если траекторией является  прямая линия, то движение точки называют прямолинейным,  а если кривая, то криволинейным.

 

         ВЕКТОРНЫЙ СПОСОБ. 

         Положение точки можно задать, как известно, и  с помощью радиуса-вектора.  При движении материальной точки  радиус-вектор, определяющий её положение,  с течением времени изменяется (поворачивается, меняет длину) см. рис….. Т.е. является функцией времени.

                                   

             Последнее есть — закон движения точки,  записанный в векторной форме.  Если он известен, то мы можем для любого момента времени рассчитать радиус-вектор точки, а значит, определить её положение.

            Таким образом, задание трех скалярных уравнений, равносильно заданию одного векторного уравнения.

 

ИТАК:

          Положение материальной точки в пространстве в любой момент времени (закон движения) можно определять либо с помощью зависимости координат от времени x = x (t), y = y (t), z = z (t) (координатный способ), либо при помощи зависимости от времени радиус-вектора 

(векторный способ), проведенного из начала координат до данной точки (рис. 1.1.1).

Рисунок 1.1.1.

Определение положения точки с помощью координат x = x (t), y = y (t) и z = z (t) и радиус-вектора  ,

– радиус-вектор положения точки в начальный момент времени.

 

 

https://www.youtube.com/watch?v=qvo5dSC-Lo0&list=PLJ8TtQgi6QOr8iN7BAbl8iwAIVUKVhIqc&index=9

 

 

Координаты.

Из курса математики вы знаете,  что положение точки можно задать с помощью координатной прямой, прямоугольной системы координат, либо трехмерной системе координат.

 

           Координатами называются числа, определяющие положение точки в пространстве.

 

         Когда  тело отсчета выбрано, через какую-нибудь его точку проводят оси координат и положение любой точки в пространстве описывают её координатами.

       Рассмотрим системы для различных представлений пространства:

 

1.   Одномерное пространство.  

 

       2. Двумерное пространство.

3. Трехмерное пространство.

ИТАК:  Перемещение — величина векторная:  а вот ссылка, где рассказывается о векторах и правилах работы с ними.

https://phyzrf.ru/bez-rubriki/o-vektornyh-velichinah

Но, кое-какие моменты рассмотрим здесь.

 

Проекции вектора перемещения

При решении задач по физике часто используют проекции вектора перемещения на координатные оси. Проекции вектора перемещения на координатные оси могут быть выражены через разности координат его конца и начала. Например, если материальная точка переместилась из точки А в точку В, то при этом вектор перемещения 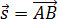 (рис. 1.3).

Выберем ось ОХ так, чтобы вектор  лежал с этой осью в одной плоскости. Опустим перпендикуляры из точек А и В (из начальной и конечной точек вектора перемещения) до пересечения с осью ОХ. Таким образом мы получим проекции точек А и В на ось Х. Обозначим проекции точек А и В соответственно А_x и В_x. Длина отрезка А_xВ_x на оси ОХ – это и есть проекция вектора перемещения на ось ОХ, то есть

S_x = A_xB_x

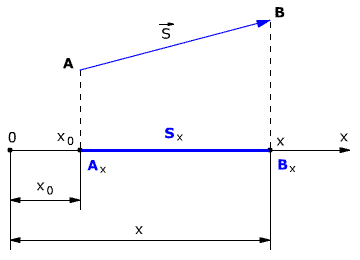
Рис. 1.3. Проекция вектора перемещения.

ВАЖНО!
Напоминаю для тех, кто не очень хорошо знает математику: не путайте вектор  с проекцией вектора на какую-либо ось (например, S_x). Вектор всегда обозначается буквой или несколькими буквами, над которыми находится стрелка. В некоторых электронных документах стрелку не ставят, так как это может вызвать затруднения при создании электронного документа. В таких случаях ориентируйтесь на содержание статьи, где рядом с буквой может быть написано слово «вектор» или каким-либо другим способом вам указывают на то, что это именно вектор, а не просто отрезок.

 

Проекция вектора перемещения на ось ОХ равна разности координат конца и начала вектора, то есть

S_x = x – x₀

Аналогично определяются и записываются проекции вектора перемещения на оси OY и OZ:

S_y = y – y_0,  S_z = z – z₀

Здесь x₀, y₀, z₀ — начальные координаты, или координаты начального положения тела (материальной точки); x, y, z — конечные координаты, или координаты последующего положения тела (материальной точки).

Проекция вектора перемещения считается положительной, если направление вектора и направление координатной оси совпадают (как на рис 1.3). Если направление вектора и направление координатной оси не совпадают (противоположны), то проекция вектора отрицательна (рис. 1.4).

Если вектор перемещения параллелен оси, то модуль его проекции равен модулю самого Вектора. Если вектор перемещения перпендикулярен оси, то модуль его проекции равен нулю (рис. 1.4).

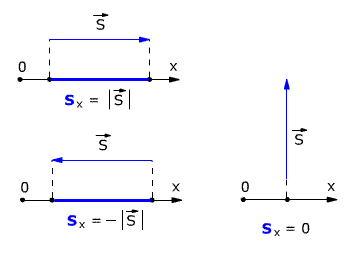
Рис. 1.4. Модули проекции вектора перемещения.

Разность между последующим и начальным значениями какой-нибудь величины называется изменением этой величины. То есть проекция вектора перемещения на координатную ось равна изменению соответствующей координаты. Например, для случая, когда тело перемещается перпендикулярно оси Х (рис. 1.4) получается, что относительно оси Х тело НЕ ПЕРЕМЕЩАЕТСЯ. То есть перемещение тела по оси Х равно нулю.

Рассмотрим пример движения тела на плоскости. Начальное положение тела – точка А с координатами х₀ и у₀, то есть А(х₀, у₀). Конечное положение тела – точка В с координатами х и у, то есть В(х, у). Найдём модуль перемещения тела.

Из точек А и В опустим перпендикуляры на оси координат ОХ и OY (рис. 1.5).

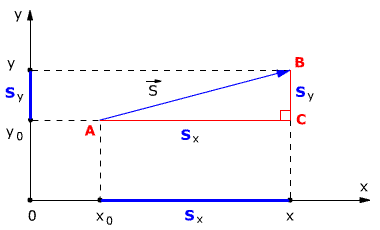
Рис. 1.5. Движение тела на плоскости.

Определим проекции вектора перемещения на осях ОХ и OY:

Sx = x – x0
Sy = y – y0

На рис. 1.5 видно, что треугольник АВС – прямоугольный. Из этого следует, что при решении задачи может использоваться теорема Пифагора, с помощью которой можно найти модуль вектора перемещения, так как

АС = sx
CB = sy

По теореме Пифагора

S2 = Sx2 + Sy2

Откуда можно найти модуль вектора перемещения, то есть длину пути тела из точки А в точку В:

 

Примечание:

(И для работы с координатами векторов, неплохо бы вспомнить кое-что из тригонометрии).

https://phyzrf.ru/bez-rubriki/o-vektornyh-velichinah

 

https://www.youtube.com/watch?v=eq2A9IX-TYM&list=PLJ8TtQgi6QOr8iN7BAbl8iwAIVUKVhIqc&index=10

---

 

ОПРЕДЕЛЕНИЕ КООРДИНАТЫ ДВИЖУЩЕГОСЯ ТЕЛА. ( § 3 П. 9кл.)

(Практический пример).

 

В большинстве случаев необходимо вычислить положение тела, т.е. определить его координаты.  Известно, что вычисление производят не с векторами, а с соответствующими им скалярными величинами: с проекциями векторов на координатные оси и с модулями векторов или их проекций (т.е. с величинами, представляющими собой положительные или отрицательные числа, но не имеющие направления). 

            Покажем, как определить координату движущегося тела, зная  координату его начального положения и вектор перемещения.  Для этого решим задачу.

 

       Два катера идут по реке в противоположных направлениях и встречаются в 100 км к востоку от пристани П (рис. 4).  Продолжая движение, за некоторый промежуток времени t   первый катер

переместился от мета встречи на 60 км к востоку, а второй — на 50 км к западу. Определите координаты каждого катера относительно пристани и расстояние между катерами через промежуток времени  t   после их встречи. 

              Проведем координатную ось ОХ  параллельно прямой, вдоль которой движутся катера, и направим её на восток.  Начало  этой оси (х=0) — точку О — совместим с пристанью,  приняв её за тело отсчета (поскольку в задаче требуется определить положение катеров по отношению к пристани).

 

 

Спроецировав начала и концы векторов перемещения     и         на ось ОХ, получим отрезки            , которые являются проекциями  указанных векторов.  Проекция вектора на ось считается положительной, если вектор сонаправлен с этой осью, и отрицательной, если вектор направлен противоположно оси. 

              Значит,  в данном случае    ,   а  .

Из рисунка 4 видно, что координаты     и      можно найти следующим образом:

(1)   

  (2)

Расстояние     между двумя телами, как известно, равно модулю разности их координат:

(3)

По  уравнениям (1) и (2) можно рассчитать искомые координаты   и . Но какие числа следует подставить  в уравнения  (1) и (2) вместо символов , и ?

             Согласно условию задачи катера встретились на расстоянии 100 км от пристани, значит, длина отрезка       равна 100 км.  Из рисунка 4 видно, что координата    находится на положительной полуоси  ОХ, т.е.       Значит,  = 100км.  Поскольку ось ОХ параллельна векторам перемещений катеров, длины проекций    и    равны соответственно длинам векторов    и     (как противоположные стороны построенных на них прямоугольников).   А это означает, что модуль каждой проекции равен модулю соответствующего ей вектора.  Указанные в задаче расстояния ( 60км и 50 км), на которые сместились катера за время t, представляют собой модули векторов их перемещений.    Значит, модуль проекции    равен  60 км, а модуль проекции     равен 50 км. 

             Поскольку проекция     положительна, то можно записать:  = 60 км. Но проекция   отрицательна,  поэтому    = — 50 км.   

            Теперь запишем условие задачи и решим её.

 

 

              Мы получили формулу, которая позволяет определить координату тела, если известны начальное положение тела и проекция его перемещения. 

 

 

ПЕРЕМЕЩЕНИЕ ПРИ ПРЯМОЛИНЕЙНОМ РАВНОМЕРНОМ ДВИЖЕНИИ. (§ 4.п. 9 кл.)

 

            Во всех рассмотренных нами примерах и задачах по определению координат тела вектор перемещения был известен (т.е. были известны его модуль и направление). 

           А как найти вектор перемещения, если он не задан?  Проще всего найти формулу для определения вектора перемещения для тела, движущегося  прямолинейно и

равномерно (т.е. движущегося по прямолинейной траектории и проходящего за любые равные промежутки времени одинаковые пути).

 

Согласно определению, 

———————————————————————————————————————————————————————

             скорость равномерного прямолинейного движения — это постоянная векторная величина, равная отношению перемещения тела за любой промежуток времени к значению этого промежутка.

---

      (1)

         Из формулы (1) можно найти перемещение для прямолинейного равно мерного движения:

(2)

         При решении  большинства  задач на нахождение векторных величин (перемещение, скорости, силы и др.) необходимо знать как эти величины направлены  по  отношению друг к другу.  Об этом можно судить, в частности, по уравнениям, записанным  в векторной форме.  Например, формулы (1) и (2) свидетельствуют о том, что при прямолинейном равномерном движении векторы  скорости

и перемещения направлены  в одну и ту же сторону.

            Но для расчёта перемещения  перемещения применяют формулу,  в которую входят проекции векторов на ось:

(3)

 

Тогда для формулы определения координатйыы тела в любой момент времени можно записать так:

 

Мы получили зависимость координаты от времени — уравнение движения тела.   

Зависимость    может быть выражена не только алгебраически, но и графически.

            Из курса математики нам известно нам известна линейная функция    ,  где х — аргумент,  k —постоянный коэффициент, b — свободный член. Графиком этой функции является прямая. 

             Функция   ,   (  или      ) тоже линейная функция

с аргументом  ,  постоянным коэффициентом     и свободным членом   .   Значит, её график — прямая.   

 

             Напомним, что по знаку проекции можно судить о том, как направлен соответствующий ей вектор по отношению к выбранной оси. Но, если при решении задач на прямолинейное движение нас не интересует направление вектора перемещения и скорости, то можно воспользоваться  формулой, в которую входят их модули:

(4)

        Формула (4) вам давно знакома — вы часто использовали её при решении задач по физике и математике.  Только под буквой s подразумевался пройденный телом путь, почему же теперь мы говорим, что s — это модуль вектора перемещения? 

      Дело в том, что при движении в одном направлении модуль вектора перемещения, совершенного телом за некоторый промежуток времени, равен пути, пройденному этим телом за тот  же промежуток времени.

               На рисунке 6 представлен график зависимости модуля вектора скорости от времени t при равномерном движении тела. С такими графиками вы уже встречались при изучении физики в 7 классе (тогда их называли графиками зависимости скорости от времени).

               Модуль вектора перемещения      , совершённого телом за промежуток времени    , в данный момент времени определяется по формуле:

 

Но произведение   1`    численно равно также и площади   S  закрашенного прямоугольника, так как отрезки    и (или, что то же самое,     и       ) являются смежными сторонами этого прямоугольника.   

            Таким образом, при прямолинейном равномерном движении тела модуль вектора его перемещения численно равен площади прямоугольника, заключенного между графиком скорости,  осью Ot и перпендикулярами к этой оси, восстановленными из точек, соответствующих моментам начала и конца наблюдения  (В данном случае из точек O и ).

Часто эту площадь называют площадью под графиком скорости.

 

Вычисление перемещения при равномерном движении:

 

 

 

 

          §3.           РАВНОМЕРНОЕ ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ. СКОРОСТЬ.

 

 

Урок физики в Ришельевском лицее

 

                  1. Равномерное прямолинейное движение — движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения. Слова «любые равные» означают, что за каждый час, за каждую минуту, за каждые 30 минут, за каждую секунду, за каждую долю секунды тело совершает одинаковые перемещения.

             При равномерном прямолинейном  (с постоянной скоростью) движении путь L может быть найден по формуле:

где: v – скорость тела, t – время в течении которого оно двигалось. При решении задач по кинематике перемещение обычно находится из геометрических соображений. Часто геометрические соображения для нахождения перемещения требуют знания теоремы Пифагора.

 

                Описывать равномерное прямолинейное движение можно как с помощью математических формул, так и графически.

        Чтобы найти координаты движущегося тела в любой момент времени, нужно, как мы видели, нужно знать проекции вектора перемещения, (а значит,  и сам вектор).  Как найти вектор перемещения? Мы рассмотрим сначала самый простой вид движения — прямолинейное равномерное движение.  Прямолинейное движение, это движение, при котором траектория тела (точки) — прямая линия.  Примером может  служить движение автомобиля по участку дороги. на котором нет подъемов, спусков, поворотов.

            А  прямолинейным равномерным движением называют такое движение, при котором тело (точка) за любые равные промежутки времени совершает одинаковые перемещения.

              Для описания прямолинейного движения удобно направить одну из координатных осей. например ось Х, вдоль той прямой, по которой движется тело.   Тогда координата х будет единственной координатой, которая изменяется при движении.  Вектор передвижения при таком выборе оси может быть  направлен либо так же, как координатная ось, либо противоположно ей.

 

 

        §4. СКОРОСТЬ.

 

         Скорость. Как найти (вычислить) перемещение тела за какой-то промежуток времени t?  Для этого нужно знать перемещение тела за единицу времени.  Если за t единиц времени совершено перемещение

, то отношение  показывает, какое перемещение совершает тело в единицу времени. Это отношение называют скоростью движения и обозначают буквой  :

                     

        Скоростью равномерного прямолинейного движения называют постоянную векторную величину, равную перемещению тела за любой промежуток времени к  значению этого промежутка.

Зная скорость , мы найдем перемещение за любой промежуток времени t.

                                           (1).

Направлен вектор скорости также, как и вектор перемещения.  Направление вектора скорости — это и есть направление движения тела.

В скалярном виде, уравнение для проекции на ось х, будет иметь вид:  .     (1.а)

Теперь. используя выражение для проекции  с начальной координаты в точке x_0,

получим выражение для проекции перемещения  S_x = x – x_{0.       (СМ. ниже  или в векторах)}

Можно вычислить координату х тела в любой момент времени t:

                                     

или

                 (2)

Таким образом мы нашли, как координата Х тела зависит от времениt . ( т.е. нашли определить положение тела в любой момент времени).  А это и есть решение основной задачи механики.  

 

Формулу (2) можно использовать и для  того, чтобы вычислить проекцию скорости тела, если нам известна  проекция Sx  перемещения.

                                (2a)

            Эта формула позволяет понять, какой смысл имеет величина «скорость».  Из неё видно, что проекция скорости на координатную ось равна изменению координаты в единицу времени.  Т.е. скорость показывает, как быстро изменяются при движении координаты тела.  Но при этом надо помнить, что проекция  скорости может быть как положительной, так и отрицательной.

 

 

 

http://www.all-fizika.com/article/index.php?id_article=221

Средняя скорость

 

               Скорость – векторная величина, характеризующая быстроту перемещения тела в пространстве. Скорость бывает средней и мгновенной.

                 При неравномерное  движении тела формула скорости приобретает  иной физический смысл: она является формулой средней скорости

 

               Как здесь показано, это отношение вектора перемещения к затраченному времени, т.е величина векторная.

               При решении большинства практических задач описывать движение с помощью этой формулы неудобно.  Например, вычисленная по  этой формуле средняя скорость  современного военного самолета — истребителя оказывается равной нулю, поскольку нулю равно его перемещение:  истребитель начинает и заканчивает движение  в одной и той-же точке на аэродроме.  В то же время  в полете, приборы этого  самолета фиксируют значение скорости, составляющие несколько тысяч километров в час.

               В практических целях удобнее применять величину, называемую средней путевой скоростью.     (Или чаще — просто  средней скоростью)      и равную отношению всего пройденного  телом пути l  ко всему затраченному на это  времени. 

             Однако средняя путевая скорость не дает точного представления о движении тела по траектории.  Так тело в определенные промежутки времени может двигаться со скоростью большей или меньшей   ,  или даже останавливаться на некоторое время.

 

(Пурышева стр. 22).

 

Средняя скорость пути – это отношение всего пути ко всему времени движения.

 

 

 

 

Средняя скорость перемещения – это отношение всего перемещения ко всему времени движения:

Эта величина направлена так же, как и полное перемещение тела (то есть из начальной точки движения в конечную точку). При этом не забывайте, что полное перемещение не всегда равно алгебраической сумме перемещений на определённых этапах движения. Вектор полного перемещения равен векторной сумме перемещений на отдельных этапах движения.

• При решении задач по кинематике не совершайте очень распространенную ошибку. Средняя скорость, как правило, не равна среднему арифметическому скоростей тела на каждом этапе движения. Среднее арифметическое получается только в некоторых частных случаях.

• И уж тем более средняя скорость не равна одной из скоростей, с которыми двигалось тело в процессе движения, даже если эта скорость имела примерно промежуточное значение относительно других скоростей, с которыми двигалось тело.

МГНОВЕННАЯ СКОРОСТЬ.

 

 

 

 

 

 

               Скорость тела  в данной точке траектории или в данный момент времени называется мгновенной скоростью.

 

Предельный переход к бесконечно малым интервалам времени.

 

 

 

 

 

              Мгновенная скорость описывает движение в данный конкретный момент времени в данной конкретной точке пространства, а средняя скорость характеризует все движение в целом, в общем, не описывая подробности движения на каждом конкретном участке.

                        Мгновенная скорость, или скорость в данной точке, равна отношению достаточно малого перемещения на участке траектории, включающем эту точку, к малому промежутку времени, в течение которого это перемещение совершается.

                Мгновенная скорость — это векторная величина.  Направление вектора мгновенной скорости совпадает с направлением движения  в данной точке. 

Иными словами, мгновенная скорость в данный момент времени – это отношение очень малого перемещения 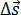 к очень малому промежутку времени, за который это перемещение произошло.

                                                      

Вектор мгновенной скорости направлен по касательной к траектории движения тела.

 

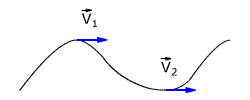
В дальнейшем, говоря о скорости неравномерного движения, мы будем иметь ввиду именно мгновенную скорость.

 

ИТАК:

Скорость – это количественная характеристика движения тела.

Средняя скорость – это физическая величина, равная отношению вектора перемещения 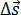 точки к промежутку времени Δt, за который произошло это перемещение. Направление вектора средней скорости совпадает с направлением вектора перемещения 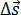. Средняя скорость определяется по формуле:

Мгновенная скорость, то есть скорость в данный момент времени – это физическая величина, равная пределу, к которому стремится средняя скорость при бесконечном уменьшении промежутка времени Δt:

 

Контрольные вопросы:

 

1. Что называется телом отсчета?
2. Какими способами можно задать положение точки? 
3. Как задают положение точки в пространстве с помощью координат?
4. Что называется радиус-вектором?
5. Что называется проекцией вектора на ось?
6. Чему равна проекция вектора на ось, если вектор направлен
так же, как и ось проекции?
7. Чему равна проекция вектора на ось, если вектор направлен
противоположно оси проекции!?
8. Чему равна проекция вектора на перпендикулярную к нему
ось?

 

Рекомендация:  Более подробно: системы отсчета, способы описания движения освещены в учебнике Мякишева и Буховцева §3, §4, §5

https://phyzrf.ru/bez-rubriki/o-vektornyh-velichinah

 

САМОЕ ВАЖНОЕ.

 

           Явление механического движения состоит в том, что положение тел относительно других тел, т.е. их координаты, с течением времени изменяются.

             Для определения положения тела (его координат) в любой момент времени нужно знать начальные значения его координат и вектор перемещения, потому что изменения координат как раз равны проекциям вектора перемещения на соответствующие координатные оси.

           Чтобы найти вектор перемещения, нужно знать скорость.

             При прямолинейном равномерном  движении  скорость — величина постоянная, равная отношению вектора перемещения тела к промежутку времени за который перемещение совершено.

            Если направить координатную ось направить вдоль прямой, по которой происходит движение (в направлении движения или против него), то положение тела определяется всего одной координатой.  Эта координата (например, х) вычисляется по формуле  ,    где  —   начальная координата и     — проекция скорости  движения    на координатную ось Х.

        Движение относительно. Это значит, что при перемещении, скорость, траектория движения  различны относительно разных систем координат.

           Относителен и покой.  Абсолютно покоящихся тел тел не существует: тело, покоящееся относительно одной системы координат, движется относительно каких-то других систем. Материя существует только в движении.

Равноускоренное движение. Ускорение. Скорость

 

 

   §5.  УСКОРЕНИЕ.  РАВНОУСКОРЕННОЕ ДВИЖЕНИЕ.

              

           При неравномерном движении мгновенная скорость тела меняется от точки к точке, от одного момента времени до другого.  Как же вычисляется мгновенная скорость?

             Мы видели раньше, что для вычисления координаты тела в любой момент времени, нужно знать, как быстро она изменяется, т.е. каково её изменение за единицу времени.  Быстрота изменения координаты равна, как мы видели,  проекции скорости на соответствующую координатную ось.  Точно так же для  вычисления скорости в любой момент времени, Нужно знать, как быстро изменяется скорость, на сколько она изменяется за единицу времени. 

 

                            Равноускоренное движение.  Для простоты мы будем рассматривать такое неравномерное движение, при котором  мгновенная скорость тела за каждую единицу времени,  и вообще за любые равные промежутки времени изменяется одинаково.  Такое движение тела называют равноускоренным.  Движение тела, при котором его  скорость за любые равные промежутки времени изменяется одинаково, называется равноускоренным движением.

            Если в некоторый начальный момент времени скорость тела равна ,  а через промежуток времени t, она окажется равной  ,  то для того, чтобы узнать насколько скорость изменилась за единицу времени,  нужно взять отношение изменения скорости       к промежутку времени   t.

 Это  отношение    и есть быстрота изменение скорости.  Её называют  ускорением.

          Ускорением тела при его равноускоренном движении называется величина, равная отношению изменения скорости к промежутку времени, в течение которого это изменение произошло.

Обозначается ускорение буквой   :

 

                                                                                                 (5,1)

 

 

           Так как ускорение равно произведению векторной величины   на скалярную , то ускорение  — величина векторная.

           Если ускорение по модулю велико, это значит. что тело быстр набирает скорость (когда оно разгоняется)   или быстро теряет скорость (при торможении).

           Зная начальную скорость тела      и его ускорение    ,   можно найти скорость      тела в любой момент времени.    Действительно из формулы (5.1) следует, что

 

                                                                                          (5,2)

 

       Уравнение для проекции вектора скорости, например, на ось Х, будет выглядеть так:

(3)

                     Единица ускорения.  

 

            Если ускорение постоянно, то его можно истолковать как изменение скорости в единицу времени.  Это позволяет установить единицы модуля ускорения и его проекций.  

              Запишем выражение для модуля ускорения:

                 Отсюда следует, что модуль ускорения численно равен единице, если за единицу времени модуль вектора изменения скорости  изменяется на единицу.

 

         Если время измерено в секундах, а скорость в метрах, то единица ускорения = 1 м/с².

 

           Так как,    то модуль  ускорения равен единице, если равен единице модуль ускорения скорости      и равен единице промежуток времени t.

 

       

 

 §6. ПЕРЕМЕЩЕНИЕ ПРИ ПРЯМОЛИНЕЙНОМ РАВНОУСКОРЕННОМ ДВИЖЕНИИ

 

 

 

Вычисление перемещения при равноускоренном движении:

 

 

 

 

 

 

 

 

 

 

            Другая формула для перемещения.  Для вычисления перемещения можно получить и другую полезную формулу, в которую время не входит.  Из выражения      получим выражение для времени    и подставим его в формулу для перемещения      приведенную выше, тогда получаем:

 

   

Отсюда

 

или

  (4)

                 Эти формулы  позволяют найти перемещение тела, если  известны ускорение, а также начальные и конечные скорости движения. Если начальная скорость   равна нулю, то формулы (4) приобретают вид:

 

               

Итак, если начальная скорость равна нулю, то пройденный путь, (координата) рассчитывается по формуле:

(21)

 

из курса математики,  — это парабола.

 

 

 

                 На рисунке дан график равноускоренного движения с начальной скоростью, равной нулю.  График построен по  формуле (21) для  значения α=2м/с².  Он изображается кривой линией, поднимающейся вверх все круче и круче.   Расстояние точек от оси времени пропорционально квадрату расстояния от оси пути.  Такая кривая называется параболой.

                    Из формулы (21) видно, что при начальной скорости равной нулю, путь, пройденный  при равноускоренном движении за первую секунду ( t=1) численно равен половине ускорения.    Если известен путь, пройденный без начальной скорости за время t, то ускорение можно найти по формуле. вытекающей из (21):

    ;

Если начальная скорость равна нулю, можно выразить путь S, пройденный к моменту  t, через  скорость    в этот момент или скорость  через пройденный путь.  Действительно, в этом случае  

и                                                                                   и

 

           Исключая   из этих выражение t,  найдем:

и

==================================================

 

              Все эти формулы переходят в формулы для равномерного движения, если положить в них ускорение, равным нулю.

                         Во всех формулах  знаки проекций векторов   ,  и , а так же знак начальной координаты определяется условием задачи и направлением координатной оси.

 

 

 

Вспомогательные ссылки:

Учебники:

 

https://yadi.sk/i/akTtpZfZjARGqA

https://yadi.sk/i/0VzZzEQvqZgkWg

 

Памятка по векторам по ссылке:

http://physics-everywhere.phyzrf.ru/mehanic/vektora-i-resheniya

 

С вопросами обращаться в «контакты».

Контакты