Вспомним самое важное из ранее пройденного материала:
САМОЕ ВАЖНОЕ:
Основная задача механики — вычисление положения тела в любой момент времени решается по своеобразной «цепочке»: чтоб найти координату точки, нужно знать её перемещение, а чтобы знать перемещение, нужно знать скорость. При прямолинейном равномерном движении используется именно эта «цепочка»: скорость → перемещение → координата.
При равноускоренном движении нужно еще знать ускорение, и «цепочка» другая: ускорение → скорость → перемещение → координата. И для равноускоренного и для равномерного движения должны быть известны начальные условия — начальная координата и начальная скорость.
При равноускоренном движении скорость непрерывно изменяется, и для нахождения скорости в любой момент времени (мгновенной скорости) нужно знать, как быстро она изменяется. Быстрота изменения скорости задается её ускорением :
Проекцию скорости на координатную ось находят по формуле
,
где — проекция начальной скорости и -проекция ускорения.
Координату вычисляют по формуле:
а проекцию перемещения — по формуле:
Итак, из ранее рассмотренной схемы, мы прошли прямолинейное, равномерное и равноускоренное прямолинейное движение.
Рассмотрим некоторые другие виды движения и методы их описания.
Вспоминаем:
Средняя скорость
Скорость – векторная величина, характеризующая быстроту перемещения тела в пространстве. Скорость бывает средней и мгновенной.
При неравномерном движении тела формула скорости приобретает иной физический смысл: она является формулой средней скорости
Как здесь показано, это отношение вектора перемещения к затраченному времени, т.е величина векторная.
При решении большинства практических задач описывать движение с помощью этой формулы неудобно. Например, вычисленная по этой формуле средняя скорость современного военного самолета — истребителя оказывается равной нулю, поскольку нулю равно его перемещение: истребитель начинает и заканчивает движение в одной и той-же точке на аэродроме. В то же время в полете, приборы этого самолета фиксируют значение скорости, составляющие несколько тысяч километров в час.
В практических целях удобнее применять величину, называемую средней путевой скоростью. (Или чаще — просто средней скоростью) и равную отношению всего пройденного телом пути l ко всему затраченному на это времени.
Однако средняя путевая скорость не дает точного представления о движении тела по траектории. Так тело в определенные промежутки времени может двигаться со скоростью большей или меньшей
, или даже останавливаться на некоторое время.
(Пурышева стр. 22).
Средняя скорость пути – это отношение всего пути ко всему времени движения.
Средняя скорость перемещения – это отношение всего перемещения ко всему времени движения:
Эта величина направлена так же, как и полное перемещение тела (то есть из начальной точки движения в конечную точку). При этом не забывайте, что полное перемещение не всегда равно алгебраической сумме перемещений на определённых этапах движения. Вектор полного перемещения равен векторной сумме перемещений на отдельных этапах движения.
-
При решении задач по кинематике не совершайте очень распространенную ошибку. Средняя скорость, как правило, не равна среднему арифметическому скоростей тела на каждом этапе движения. Среднее арифметическое получается только в некоторых частных случаях.
-
И уж тем более средняя скорость не равна одной из скоростей, с которыми двигалось тело в процессе движения, даже если эта скорость имела примерно промежуточное значение относительно других скоростей, с которыми двигалось тело.
МГНОВЕННАЯ СКОРОСТЬ.
Скорость тела в данной точке траектории или в данный момент времени называется мгновенной скоростью.
Мгновенная скорость описывает движение в данный конкретный момент времени в данной конкретной точке пространства, а средняя скорость характеризует все движение в целом, в общем, не описывая подробности движения на каждом конкретном участке.
Мгновенная скорость, или скорость в данной точке, равна отношению достаточно малого перемещения на участке траектории, включающем эту точку, к малому промежутку времени, в течение которого это перемещение совершается.
Мгновенная скорость — это векторная величина. Направление вектора мгновенной скорости совпадает с направлением движения в данной точке.
Иными словами, мгновенная скорость в данный момент времени – это отношение очень малого перемещения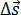 
к очень малому промежутку времени, за который это перемещение произошло.
Вектор мгновенной скорости направлен по касательной к траектории движения тела.
В дальнейшем, говоря о скорости неравномерного движения, мы будем иметь ввиду именно мгновенную скорость.
ИТАК:
Скорость – это количественная характеристика движения тела.
Средняя скорость – это физическая величина, равная отношению вектора перемещения 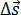точки к промежутку времени Δt, за который произошло это перемещение. Направление вектора средней скорости совпадает с направлением вектора перемещения 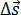. Средняя скорость определяется по формуле:
Мгновенная скорость, то есть скорость в данный момент времени – это физическая величина, равная пределу, к которому стремится средняя скорость при бесконечном уменьшении промежутка времени Δt:
Данные характеристики — мгновенная скорость, средняя скорость, средняя путевая скорость применимы и к другим видам механического движения.
==================================================
А теперь:
Рассмотрим еще один вид равнопеременного движения: свободное падение тел.
СВОБОДНОЕ ПАДЕНИЕ ТЕЛ. Ускорение свободного падения.
Рассмотрим теперь одно часто встречающееся движение с постоянным ускорением. которое называется свободным падением тел. Это движение опытным путем изучал великий итальянский ученый Галилео Галилей.
Каждый из нас наблюдал, что при падении тела на Землю из состояния покоя, оно увеличивает скорость. т.е. движется с ускорением. Это ускорение сообщает ему земной шар. Долгое время считали, что Земля сообщает различным телам различные ускорения. Простые наблюдения как будто подтверждают это. Например, птичье перо или лист бумаги падают гораздо медленнее, чем камень.
Вот почему со времен Аристотеля (греческого ученого, жившего в IVв. до н. э.) считалось незыблемым мнение, что ускорение, сообщаемое Землей телу, тем больше, чем тяжелее тело.
Только Галилею в конце XVI в. удалось опытным путем доказать. что это не так. Нужно учитывать сопротивление воздуха. Именно оно искажает картину свободного падения тел, которую можно было бы наблюдать в отсутствии земной атмосферы.
Наблюдая падения разных тел со знаменитой Пизанской башни, Галилей доказал, что земной шар сообщает всем телам одно и то же ускорение. Все тела достигали поверхности Земли примерно за одно и то же время. Особенно был прост и убедителен опыт, проведенный впервые Ньютоном.
В стеклянную трубку помещают различные предметы: дробинки, кусочки пробки, пушинки и т. д. Если перевернуть трубку так, чтобы эти предметы могли падать, то быстрее всего упадет дробинка, за ней — кусочек пробки и, наконец, плавно опустится пушинка. Но если выкачать из трубки воздух, то мы увидим, что все три тела упадут одновременно. Значит, движение пушинки задерживалось ранее сопротивлением воздуха, которое в меньшей степени сказывалось на движении, например, пробки.
Когда же на эти тела действует только притяжение к Земле, то все они падают с одним и тем же ускорением.
Движение тела только под влиянием притяжения его к Земле, называют свободным падением.
Соответственно этому и ускорение, сообщаемое Землей всем телам, называют ускорением свободного падения.
Оно всегда направлено вертикально вниз, Его принято обозначать буквой
§3. ДВИЖЕНИЕ С ПОСТОЯННЫМ УСКОРЕНИЕМ СВОБОДНОГО ПАДЕНИЯ.
При изучении свободного падения тел мы будем рассматривать только такие движения, при которых ускорение свободного падения постоянно, т.е. сопротивление воздуха можно не учитывать.
Эти движения будут описываться известными кинематическими уравнениями.
Движение с постоянным ускорением может быть как прямолинейным, так и криволинейным. Когда начальная скорость точки равна нулю или же направлена вдоль той же прямой, что и ускорение, то точка движется прямолинейно, вдоль этой прямой. Если начальная скорость и ускорение не направлены по одной прямой, точка движется криволинейно.
Ускорение свободного падения направлено вертикально вниз. Поэтому тело движется прямолинейно, если его начальная скорость равна нулю или направлена вдоль по вертикали
(рис. 1.34). В противном случае траектория тела будет криволинейной.
С движением тел, получивших начальную скорость под углом к ускорению свободного падения, приходится встречаться довольно часто Например: снаряд, выпущенный под углом к горизонту; ядро, которое толкнул спортсмен.
Найдем траекторию тела, брошенного под углом к горизонту, при условии, то на всем пути его движения ускорение свободного падения остается постоянным. Пусть из точки О брошено тело с начальной скоростью под углом
к горизонту (рис. 1.35). Выберем оси координат так, чтобы векторы
и были расположены в какой-либо координатной плоскости, например, в плоскости XOY. Ось OX направлена горизонтально, а ось OY — вертикально вверх. Начало координат берем в точке бросания.
Так как ускорение свободного падения с течением времени не меняется, то движение тела в данном случае, как и любое движение с постоянным ускорением можно описать уравнениями
При выборе начала координат и . Проекцию вектора на какую-либо ось можно выразить через модуль вектора и косинус угла, который этот вектор образует с положительным направлением оси. Из рисунка 1.35 видно, что и Поэтому уравнения (1.17) и (1.18) можно записать в виде:
,
(1.19)
(1.20)
Для построения траектории тела можно найти из уравнений (1.19) и (1.20) значения координат и для различных моментов времени, а затем по координатам построить точки и соединить их плавной линией.
Однако удобнее найти уравнение траектории, т.е. зависимость от . Чтобы получить это уравнение, нужно исключить время из уравнений (1.19) и (1.20).
Из уравнения (1,19) имеем
Следовательно,
Из курса алгебры известно, что графиком функции (1.21) является парабола, ось симметрии которой — прямая параллельная оси У. Поск4ольку в данном случае b, то ветви параболы направлены вниз. На рисунке 1.36 изображена парабола для случая b=-0,2м¯¹ и с — 1.6. Итак, мы доказали, что если ускорение свободного падения постоянно, то тело, брошенное под углом к горизонту, движется по параболе. Теперь выясним, какой будет траектория тела, если его начальная скорость направлена горизонтально.
Из рисунка 1.36 видно, что начиная с того момента, когда скорость тела горизонтальна, оно движется по ветви параболы. Следовательно, любое тело, брошенное горизонтально, будет двигаться по одной из ветвей параболы, вершина которой будет находиться в точке бросания. (рис. 1.37).
Наглядное представление о траектории тела, брошенного горизонтально или под углом к горизонту, можно получить на простом опыте. (рис. 1.38). Так как каждая частиц воды движется по параболе, то струя воды имеет форму параболы. В этом легко убедиться, поставив за струей экран с заранее вычерченной параболой.
При определенной скорости истечения воды, струя будет располагаться вдоль вычерченной параболы.
Мы получили формулы, позволяющие определить положение тела, брошенного под углом к горизонту и движущегося под действием силы тяжести в любой момент времени.
Что такое свободное падение? Свободное падение тела — это движение с постоянным ускорением, а именно ускорением свободного падения. Силой сопротивления, действующей на тело в воздухе, при рассмотрении свободного падения пренебрегаем. Отсюда следует: для того чтобы движение можно было считать свободным, необходимо, чтобы скорости движения были невелики и такая форма тел, при которой сила сопротивления воздуха была бы мала. Из видео об свободном падении: Движение тела происходит по криволинейной траектории. Движение сложное. Как мы видим из видео, его можно рассматривать как сумму двух движений. Посмотрим на движение шарика сверху. Мы видим, что он движется вдоль прямой равномерно. Если посмотреть на это движение сбоку, то мы увидим, что он поднимается, а потом ускоренно падает вниз. Таким образом движение шарика можно рассматривать как сумму двух независимых движений — равномерного и ускоренного. Учебник (Физика 10 класс. Мякишев)
Движение тела, брошенного под углом к горизонту.
Бросок под углом к горизонту.
Урок 30. Графическое представление РУД
Урок 31. Решение задач на графики РУД
Урок 32. Решение задач на графики РУД (продолжение).
Урок 37. Движение тела, брошенного под углом к горизонту (начало)
https://www.youtube.com/watch?v=avmeynFLld0&list=PLCIHSgEESIz8xpNTgNEmcT1B9yVjf3eNL&index=7
§4. КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ.
Криволинейное движение более сложное, чем прямолинейное.
И в природе и в технике очень часто встречаются движения, траектории которых представляют не прямые, а кривые линии. Это — криволинейные движения.
По криволинейным траекториям движутся в космическом пространстве планеты и искусственные спутники Земли. А на Земле всевозможные средства транспорта, воды рек. воздушные атмосферные массы и т.д.
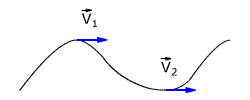
Криволинейное движение сложнее прямолинейного. При таком движении уже нельзя сказать, что изменяется только одна координата. Если, например, движение происходит на плоскости, как это видно из рисунка,
изменяются две координаты, — х и у. Непрерывно изменяется направление движения, т.е. вектора скорости, а значит, и вектора ускорения. Могут изменяться и модули скорости и ускорения. Все это делает криволинейное движение много сложнее прямолинейного.
§ 4.1. ПЕРЕМЕЩЕНИЕ И СКОРОСТЬ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ.
При прямолинейном движении направление вектора скорости всегда совпадает с направлением перемещения. А что можно сказать о перемещении и скорости в случае криволинейного движения?
Как его описать?
Перемещение по хордам.
На рис. 51 представлена некоторая криволинейная траектория. Допустим, тело движется по ней из точки А в точку В. Пройденный при этом путь — это длина дуги АВ, а перемещение это вектор направленный по хорде АВ. Теперь мы не можем сказать, что скорость всегда направлена вдоль вектора перемещения. Но проведем между точками А, В ряд хорд и представим себе, что тело движется именно по этим хордам. На каждой из них тело движется прямолинейно , и вектор скорости направлен вдоль хорды, т.е. вдоль вектора перемещения (рис.52).
Мгновенная скорость — по касательной.
Сделаем наши прямолинейные участки более короткими. (рис 53). По-прежнему вектор скорости на каждом их них направлен вдоль хорды. Но видно, что эта ломаная линия все больше походит на плавную кривую.
Продолжая уменьшать длину прямолинейных участков (и, конечно, увеличивая их число), мы как бы стягиваем их в точки и ломаная линия превращается в плавную кривую. Скорость же в каждой точке направлена по касательной к этой точке.
Мгновенная скорость тела в любой точке криволинейной траектории направлена по касательной в этой точке.
В том, что скорость при криволинейном движении действительно направлена по касательной, убеждает нас. например, работа на точиле (рис.55). Если прижать к вращающемуся точильному камню конец стального прутка, то раскаленные частицы, отрывающиеся от камня, будут видны в виде искр, эти частицы летят с той скоростью, с какой они обладали в момент отрыва от камня.
Хорошо видно. что направление движения искр совпадает с касательной к окружности в той точке, где пруток касается камня. По касательной направлены и брызги от колес буксующего автомобиля (рис.56).
Таким образом мгновенная скорость в разных точках криволинейной траектории имеет различные направления, как это показано на рис. 57 или изменяться от точки к точке (рис. 58).
Но даже если по модулю скорость не изменяется, её все же нельзя считать постоянной. Ведь скорость величина векторная. А для векторных величин модуль и направление одинаково важны.
Поэтому криволинейное движение, — это всегда движение с ускорением, даже если по модулю скорость постоянна. Мы ограничимся рассмотрением именно такого криволинейного движения — криволинейного движения с постоянной по модулю скоростью. Его называют криволинейным равномерным движением. Ускорение при таком движении связано с изменением направления скорости. Как направлено и чему равно это ускорение?
Криволинейное движение — движение по дугам окружностей. Изменение скорости при криволинейном движении должно конечно зависеть от формы траектории. А различных форм кривых — бесконечное множество. Но, оказывается, не нужно рассматривать движение по каждой отдельной кривой.
На рисунке 59 показана некоторая сложная криволинейная траектория. Из рисунка видно, что отдельные части криволинейной траектории представляют собой приблизительно дуги окружностей, изображенных штриховой линией, например, участок KL — это дуга окружности малого радиуса, а участок EL — это дуга окружности большого радиуса.
Выходит, что движение по любой криволинейной траектории можно приближенно представить. как движение по дугам некоторых окружностей. Поэтому задача нахождения ускорения при равномерном криволинейном движении сводится к отысканию ускорения при равномерном движении по окружности.
§ 4.2. Ускорение при равномерном движении по окружности.
движение по окружности
Движение тела по окружности или дуге окружности довольно часто встречается в природе и технике. Приблизительно по окружности движется Луна вокруг Земли; каждая точка земной поверхности движется движется по окружности вокруг земной оси; дуги окружности описывают различные точки самолета во время виража, автомобиля при повороте, поезда а закруглении дороги и т.д. Поэтому знакомство с таким движением имеет большое значение. Рассмотрим равномерное движение по окружности.
https://www.youtube.com/watch?v=qs6WTCmrE88&list=PLCIHSgEESIz8xpNTgNEmcT1B9yVjf3eNL&index=1
Равномерное движение по окружности, — это движение с ускорением, хотя по модулю скорость не изменяется. Наша задача выяснить, как направлено и чему равно это ускорение.
Вектор ускорения направлен к центру. Ускорение, как известно, определяется равенством: (1)
Обозначим для краткости разность двух скоростей, т.е. её изменение , через , тогда
(2).
Ясно, что вектор направлен так же, как и вектор , т.к. t — величина скалярная.
Допустим, тело движется по окружности радиуса r и в некоторый момент времени, который мы примем за начальный (t=0), оно находится в точке А (рис 60).
Скорость в этой точке направлена по касательной. Рассмотрим еще одну точку, очень близкую к А, — точку В, в которой тело, двигаясь по окружности, окажется через очень малый промежуток времени t. Будем считать, что точки А и В настолько близки друг к другу, что дуга , неотличима от хорды АВ, хотя на рисунке это не получается изобразить. Но. как бы точка А не была близка к точке В, скорость в точке В все же отличается от направлением, хотя не отличается от неё по модулю . Теперь мы можем найти вектор : перенесем вектор параллельно самому себе так, чтобы он и вектор исходили из одной точки А и соединим концы обеих векторов отрезком прямой, направив его от к . Получившийся направленный отрезок и есть вектор . Из рисунка видно, что вектор направлен внутрь окружности. Если точки А и В будут предельно близки друг к другу, то вектор , перенесенный в точку А, будет направлен к центру окружности. Туда же будет направлен и вектор ускорения .
Таким образом, при равномерном движении тела по окружности, его ускорение во всех точках окружности направлено к центру. Его так и называют — центростремительным ускорением. Обозначим его .
Ускорение тела, равномерно движущегося по окружности в любой её точке, центростремительное, т.е направлено по радиусу к её центру. В любой точке вектор ускорения перпендикулярен вектору скорости. Эта особенность вектора ускорения при равномерном движении по окружности показана на рис. 61.
Чему равен модуль центростремительного ускорения?
Числовое значение (модуль) ускорения мы легко найдем из рисунка 60. Треугольник составленный из векторов, и , равнобедренный, т.к. =. Треугольник ОАВ на том же рисунке — тоже равнобедренный, потому что стороны ОА и ОВ — радиусы окружности. Углы при вершинах обоих треугольников равны. т.к. они образованы взаимно перпендикулярными сторонами.
и . Поэтому треугольники подобны, как равнобедренные с равными уаглми при вершинах. Из подобия треугольников следует пропорциональность сходственных сторон:
Здесь и модули скорости и изменения скорости пери переходе из точки А в В, r — радиус окружности. Но, как указывалось выше, если точки А и В очень близки друг к другу, то хорда АВ неотличима от дуги АВ Длина же дуги АВ — это путь пройденный телом с постоянной по модулю скоростью . Он равен . Поэтому можно написать:
, или (4.1)
Так как рассматриваемый нами промежуток времени очень мал, то и есть модуль ускорения, следовательно,
(4.2)
При равномерном движении по окружности скорость и ускорение точки не меняются по модулю.
В любой момент времени скорость направлена по касательной к окружности, а ускорение — к её центру. В этом случае связь между модулем ускорения точки, модулем её скорости и радиусом окружности R выражается формулой (4.2).
Равномерное движение точки по окружности является движением с переменным ускорением, так как укоренение непрерывно меняется по направлению.
Таким образом, при равномерном движении по окружности во всех её точках ускорение по модулю одно и то же — , но направлено оно всегда по радиусу к центру (см. рис. 61). Так что направление ускорения от точки к точке изменяется.
Напомним, что равномерное движение по окружности нас интересовало потому, что всякое движение по криволинейной траектории можно представить как движение по дугам окружностей различных радиусов. Теперь мы можем сказать, что в любой точке криволинейной траектории тело движется с ускорением, направленным к центру той окружности, частью которой является участок траектории. содержащей эту точку. Модуль же ускорения зависит от скорости тела и от радиуса соответствующей окружности.
На рис. 62 показана некоторая сложная траектория, по которой движется тело, и центростремительные ускорения в различных её точках.
ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА. УГЛОВАЯ И ЛИНЕЙНАЯ СКОРОСТИ ВРАЩЕНИЯ.
Вращательное движение вокруг неподвижной оси — еще один частный случай движения твердого тела.
Вращательным движением твердого тела вокруг неподвижной оси называется такое его движение при котором все точки тела описывают окружности, центры которых находятся на одной прямой, называемой осью вращения, при этом плоскости, которым принадлежат эти окружности, перпендикулярны оси вращения.(рис. 2.4). В технике такой вид движения встречается очень часто: например вращение валов двигателей и генераторов, турбин и пропеллеров самолетов.
Угловая скорость. Каждая точка вращающегося вдоль оси тела, проходящей через точку О, движется по окружности, и различные точки проходят за время различные пути. Так , поэтому модуль скорости точки А больше чем у точки В (рис. 2.5). Но радиусы окружностей поворачиваются за время на один и тот же угол . Угол φ — угол между осью ОХ и радиус-вектором , определяющим положение точки А (см. рис. 2.5).
Пусть тело вращается равномерно, т.е. за любые равные промежутки времени поворачивается на одинаковые углы. Быстрота вращения тела зависит от угла поворота радиуса-вектора, определяющего положение одной из точек твердого тела за данный промежуток времени; она характеризуется угловой скоростью. Например,
если одно тело за каждую секунду поворачивается на угол π/2 , а другое на угол π/4, то мы говорим, что первое тело вращается быстрее второго в два раза.
Угловой скоростью тела при равномерном вращении по окружности называется величина, равная отношению угла поворота вращающегося тела Δφ к промежутку времени Δt, за который этот поворот произошел.
Будем обозначать угловую скорость греческой буквой ω (омега). Тогда, по определению,
(4.3)
Угловая скорость выражается в радианах в секунду, (рад/сек).
(За единицу угла принимают угол между двумя радиусами круга, вращающими на окружности дугу, длина которой равна радиусу. ЭТО РАДИАН.
2π рад=360°;
1 рад.=180°/π=57°18’
1°=π/180 рад.)
Полный оборот по окружности 2π рад. Исходя из этого, угловая скорость:
ω=2πn, или ω=2πν
или
где n (ν) — число оборотов в секунду. Т.е. угловую скорость можно выразить через частоту вращения, т.е. число полных оборотов за секунду. Если тело совершает ν (греческая буква «ню») оборотов за 1 секунду (или n), то время одного оборота равно 1/ν секунд. Это время называют периодом вращения и обозначают буквой Т.
Таким образом, связь между частотой и периодом вращения можно представить в виде:
Полному обороту тела соответствует угол Δφ=2π, поэтому согласно формуле 4.3,
Если при равномерном вращении угловая скорость известна, то угол поворота:
Связь между линейной и угловой скоростью.
Скорость точки, движущейся по окружности, часто называют линейной скоростью, чтобы отличить её от угловой скорости.
Между линейной и угловой скоростью при движении по окружности существует связь. Установим её.
Точка, лежащая на окружности радиуса R, за один оборот пройдет путь 2πR. Поскольку время одного оборота есть Т, то модуль линейной скорости можно выразить так:
(4.4)
Т.к. , или , то
(4.5)
Модуль ускорения точки тела, движущейся равномерно по окружности, можно выразить через угловую скорость тела и радиус окружности.
Следовательно,
(4.6)
рок 43. Криволинейное движение. Равномерное движение по окружности. Центростремительное ускорение.
Урок 44. Вращение твердого тела. Линейная и угловая скорость. Период и частота вращения.
§ 4.3. ПЕРИОД И ЧАСТОТА ОБРАЩЕНИЯ.
Мы рассмотрели выше движение по окружности и основные определяющие его физические величины: линейную и угловую скорость, ускорение, а также методы их нахождения и связи между ними.
Одной из характеристик при движении по окружности является промежуток времени, за который тело совершает один полный оборот. Это — период вращения, или период обращения; Обозначают её буквой Т.
Так, например, в сообщениях о запуске очередного искусственного спутника Земли, указывается именно период его обращения, а не его скорость движения по орбите. Но если известно Т, то легко найти и скорость . Действительно, за время Т. Действительно, за время, равное периоду Т, тело проходит путь, равный 2πR, отсюда, как уже было показано, получаем:
Где R — радиус окружности, по которой движется тело.
Подставив это выражение в (4.2), получим:
(4.7).
Движение тела (точки) по окружности можно характеризовать еще одной величиной — числом оборотов по окружности в единицу времени. Её называют частотой обращения и обозначают буквой n или ν («ню»). Она очень просто связана с периодом обращения Т. Если, например, период обращения равен 0,1 сек, то за одну секунду тело совершает 10 оборотов.
Так что частота, — это величина обратная периоду.
Единица частоты — или .
Соответственно, скорость движения по окружности и центростремительное ускорение можно выразить через частоту.
или
:
Мы выразили скорость и ускорение при движении по окружности не только через обычные понятия скорости, но и через угловую скорость и через частоту обращения. Все эти формулы правомерны, дадут один и тот же результат при решении задач, просто показывают движение по окружности при помощи разных характеристик. Но выводятся все эти формулы одна из другой. А задачи можно решать с помощью любых из приведенных формул.
КАК ИЗМЕНЯЮТСЯ КООРДИНАТЫ ТЕЛА СО ВРЕМЕНЕМ ПРИ РАВНОМЕРНОМ ДВИЖЕНИИ ПО ОКРУЖНОСТИ.
Допустим, что некоторое тело равномерно вращается по окружности радиусом R. Систему координат удобно (хотя и не обязательно) выбрать так, чтобы начало координат совпадало с центром окружности, а оси Х и У были направлены вдоль двух взаимно перпендикулярных диаметров. Пусть при своем движении тело находится в точке М на окружности. Координата х в этот момент равна отрезку ОА на горизонтальном диаметре, а координата у — отрезку ОВ на вертикальном.
Координаты повторяются. Через промежуток времени равный времени обращения Т, тело снова окажется в точке М и его координаты х и у будут снова равны ОА и ОВ соответственно.
Такими же они будут и через два периода, и через три периода и т.д. Это и есть главная особенность движения по окружности — координаты тела через каждый период тела повторяются.
Равномерное движение по окружности — это периодическое движение.
Из того, что мы уже знаем о скорости и ускорении тела равномерно движущегося по окружности, ясно, что эти величины тоже изменяются периодически: через каждый период повторяются и численные значения и направления скорости и ускорения.
Такого рода периодические изменения величин называют колебаниями.
САМОЕ ВАЖНОЕ.
При криволинейном движении тела (материальной точки) непрерывно изменяется направление вектора скорости. В каждой точке траектории вектор скорости направлен по касательной к траектории в этой точке. Поэтому, даже равномерное движение (с постоянной по модулю скоростью) по криволинейной траектории есть движение ускоренное.
Движение тела по окружности характеризуется не только скоростью , но и периодом обращения Т и частотой обращения n (ν), и угловой скоростью ω.
ω=2πn
Где R — радиус окружности.
При равномерном движении тела по окружности, вектор вектор ускорения в любой её точке направлен перпендикулярно вектору скорости к центру окружности. Поэтому его называют центростремительным ускорением. Модуль центростремительного ускорения связан с , Т, ω и n соотношениями:
Координаты тела, движущегося равномерно по окружности, зависят от времени так, что они через промежуток времени, равный периоду обращения, повторяют свои значения. То же относится к модулям и направлениям векторов скорости и ускорения.
Подборка формул